来源：3D科研绘图

大家好，我是独孤嘌呤。

今天我们来研究一下C4D中的运动样条，更准确地说，是Turtle模式的运动样条。很多人只知道有这么个东西，却不知道怎么用，希望今天这篇教程能对你有所帮助。

图片源自百度图片

Turtle意思是海龟，那啥叫“海龟”模式的运动样条呢？简单理解就是，让一只海龟按照给定的指令爬行，最终得到的爬行路径就是Turtle模式运动样条。

所以，我们要先搞清楚，C4D中可以输入哪些指令？

当我们打开C4D，创建运动样条对象，并将其「模式」改为Turtle之后，看到的样条是这样的——

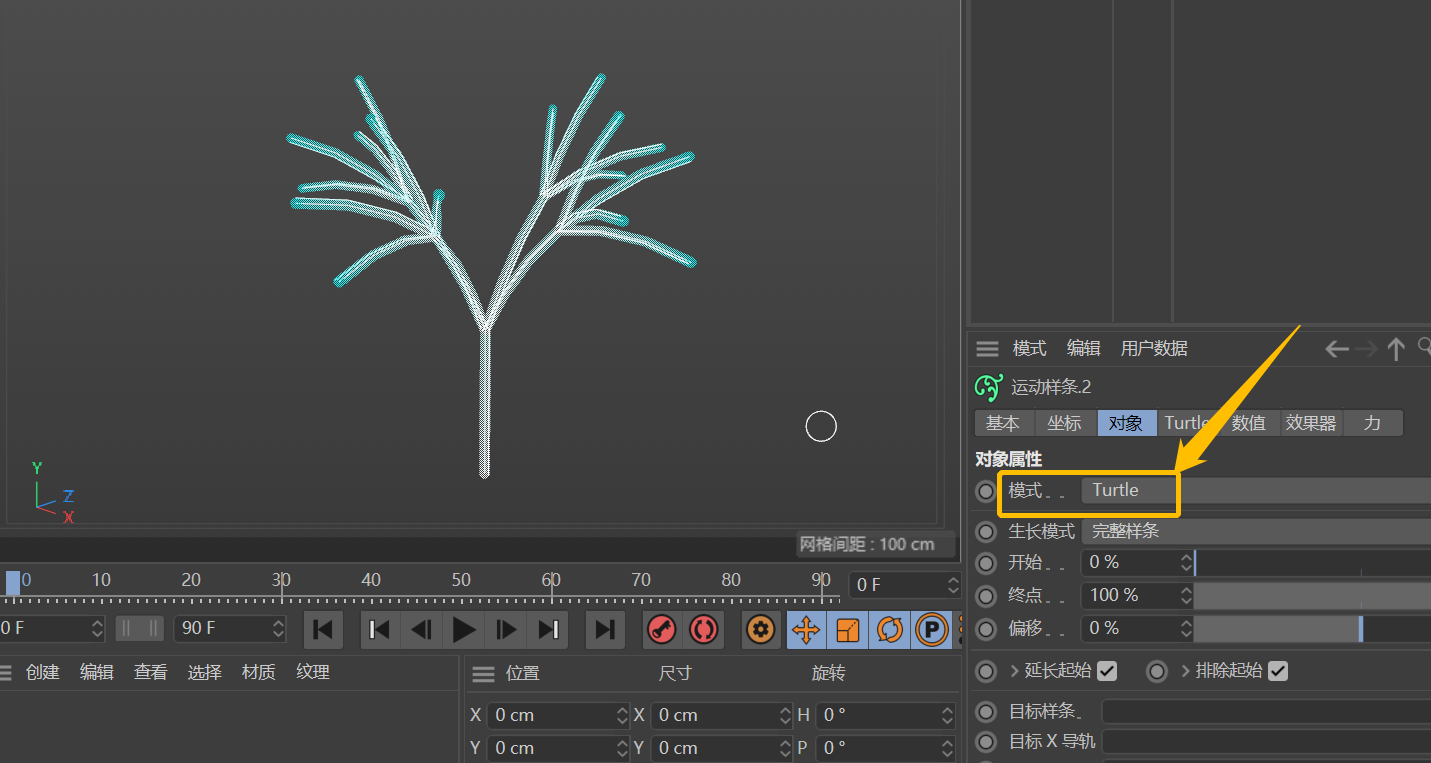
切换到Turtle属性，映入眼帘的是一串莫名其妙的字母和符号（先不要管是什么意思），这就是指令。

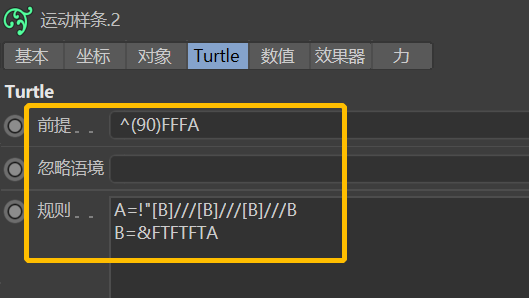
这套指令是由生物学家Lindenmayer于1968年提出的一个数学模型，被广泛应用于植物生长过程的研究。简称L-systems。

在L-systems中，有两个关键性的概念：axiom（公理）和rules（规则）。也就是Turtle属性中的「前提」和「规则」。

「前提」定义了整个样条的形状，「规则」相当于样条绘制过程中的约束条件。我们想象，有一只海龟正趴在沙滩上晒太阳。这时候有个人发出指令：往前爬1米。最终得到的就是一根1米长的直线段。对应的指令为F，意为forward。

所以，我们只需要在「前提」栏输入F，就可以得到一段直线。为了显示更清楚，这里我将数值中的「默认缩放」改为了0.1cm（也可以直接改为0）。

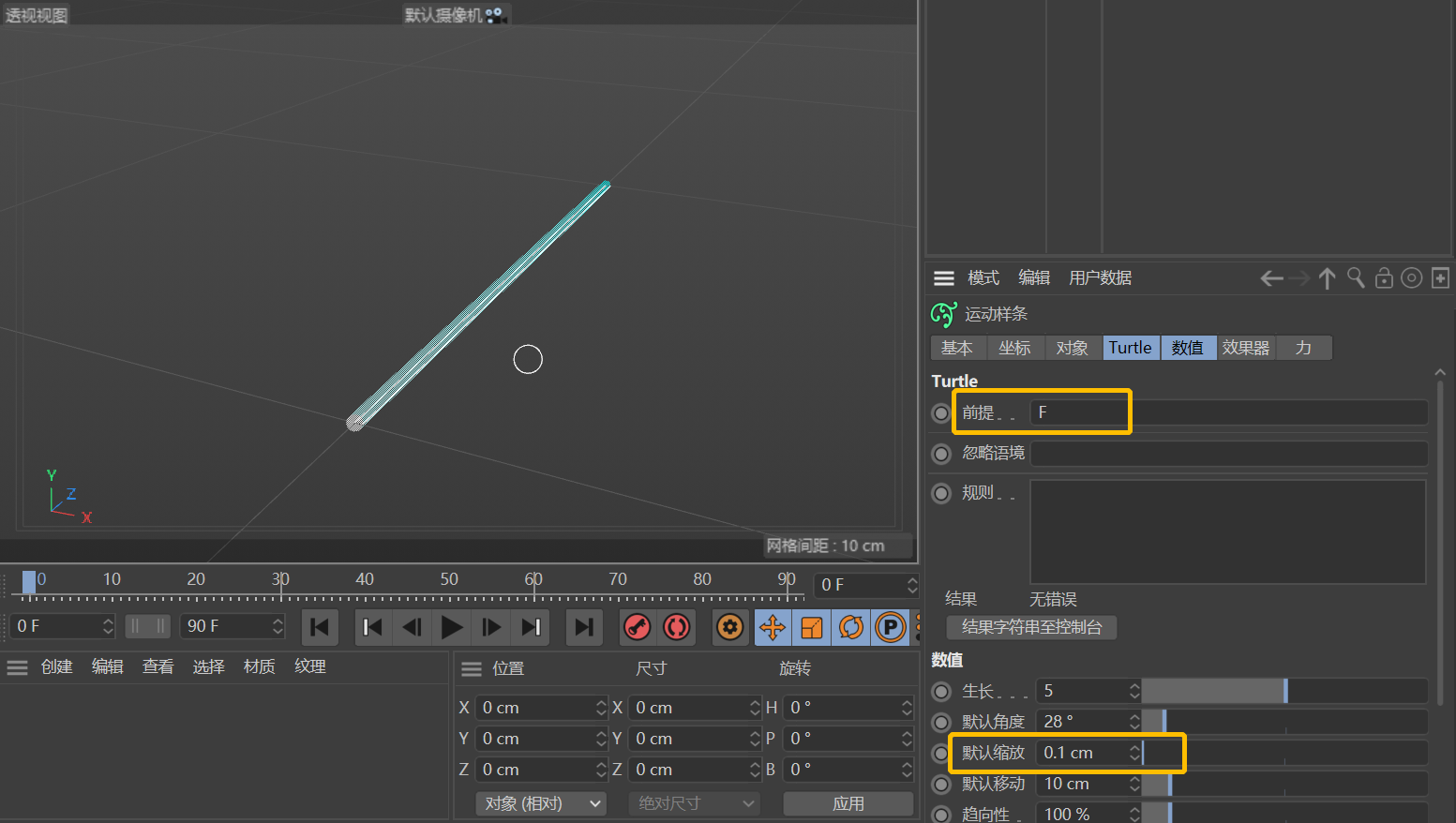
除了往前爬之外，还要告诉海龟怎么拐弯。这也很简单，-代表往左，+代表往右。

例如：F+F+F，表示往前爬一格（F），向右拐（+），再往前爬一格（F），再向右拐（+），再往前爬一格（F）。一格的长度由「默认移动」值决定，每次拐的角度则由「默认角度」决定。

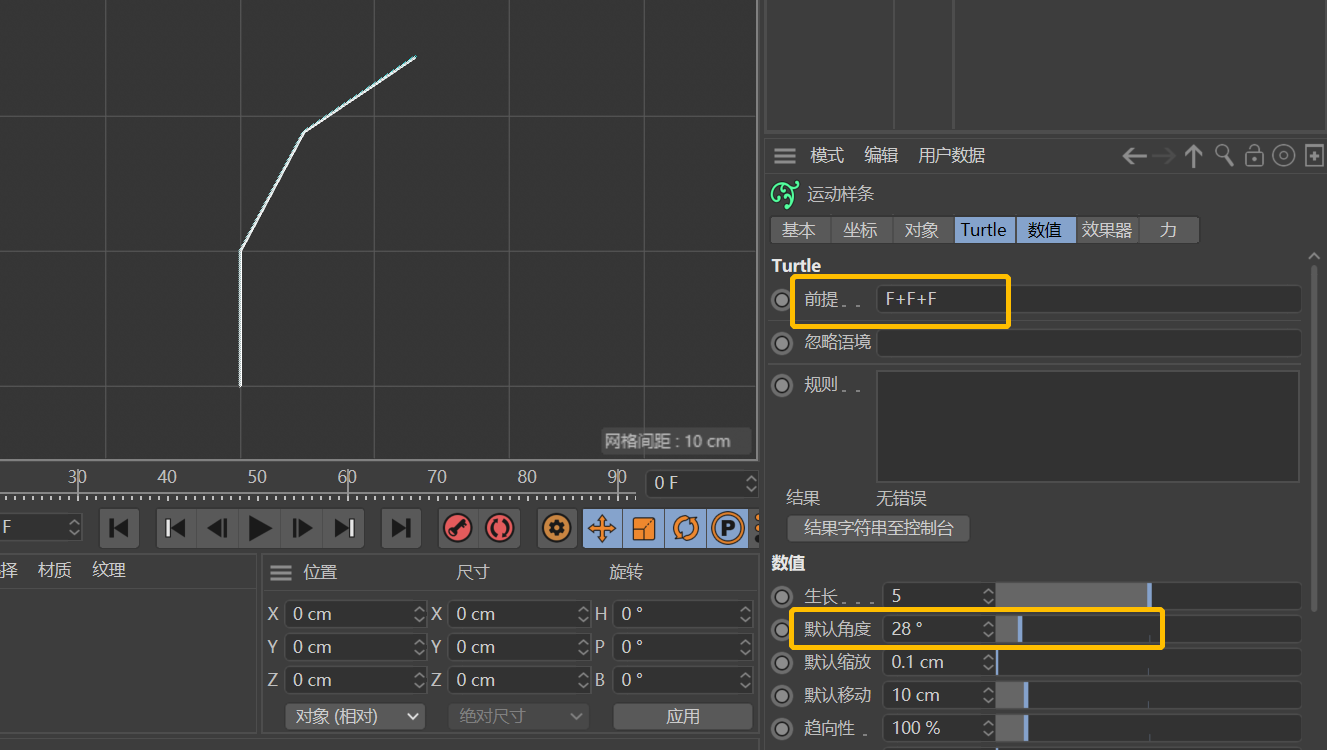
如果将「默认角度」改为90°，在「前提」栏输入F-F-F-F，将会得到什么形状呢？

答案是一个正方形。

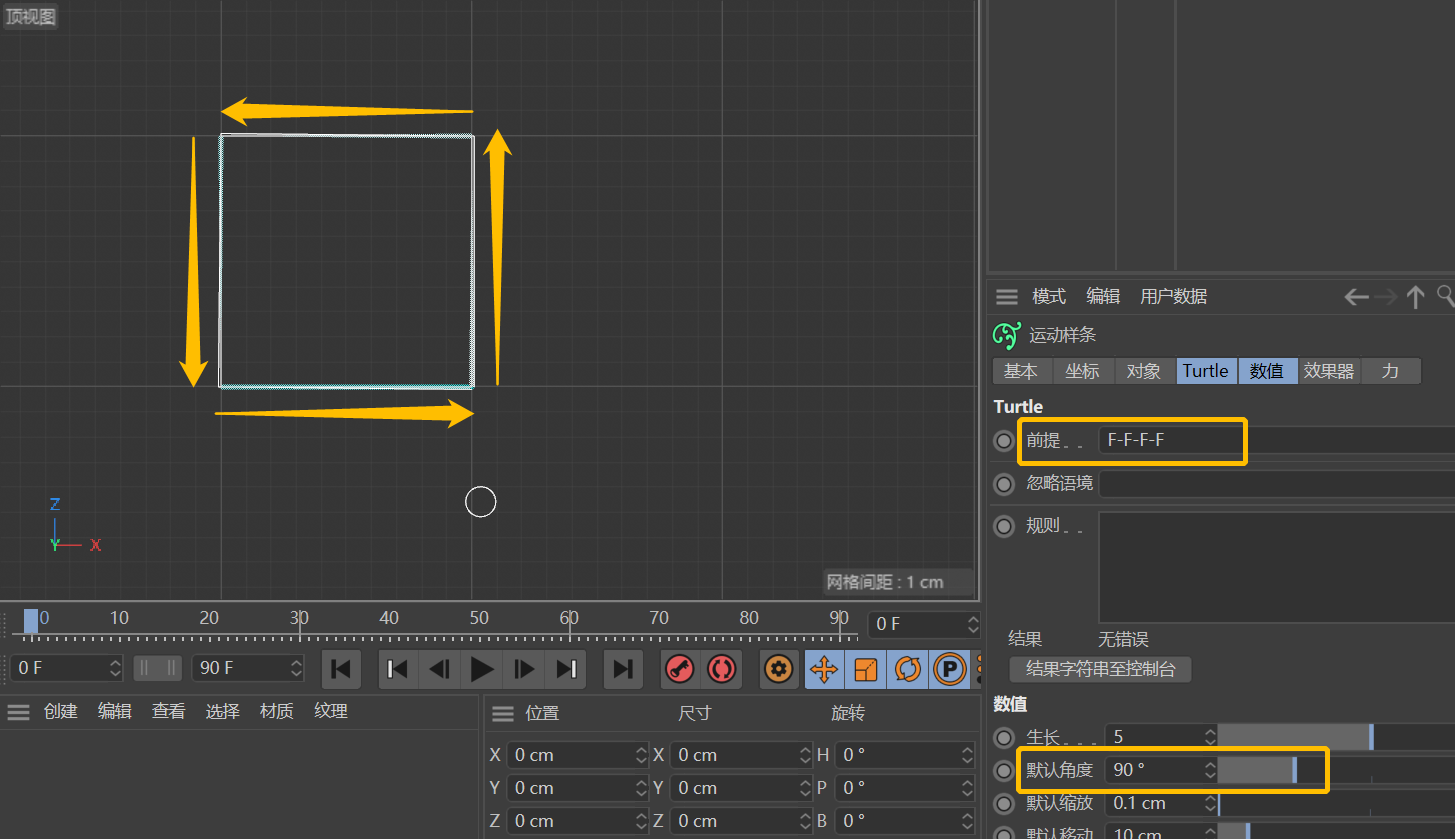
好像并没有很难是不是？我们接着往下看。

刚才只是设定了「前提」，接下来我们设置「规则」。「前提」仍为F-F-F-F，「规则」栏输入F=F-(45)F+(45)F。

-和+还是表示向左和向右，(45)规定了左拐或右拐的角度。上述规则意为：将每个F替换成了前进一格，左拐45°再前进一格，右拐45°再前进一格这样三步。最终得到的图形如下（注意这里的「生长」数值设为2）。

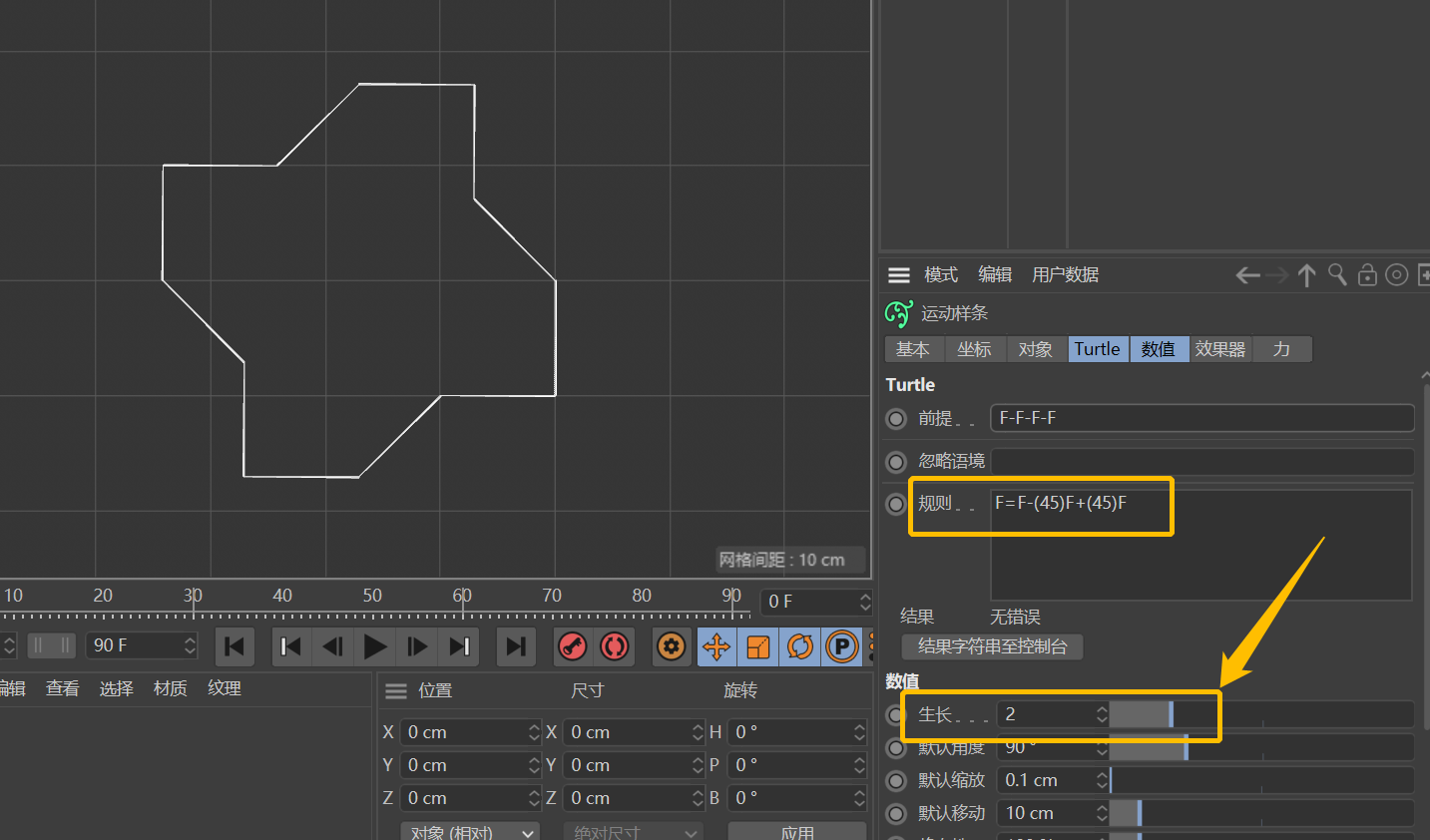
当我们将「生长」数值设为3时，就会发现整个路径的走势虽然没有变，但每一步又被分成了三小步。

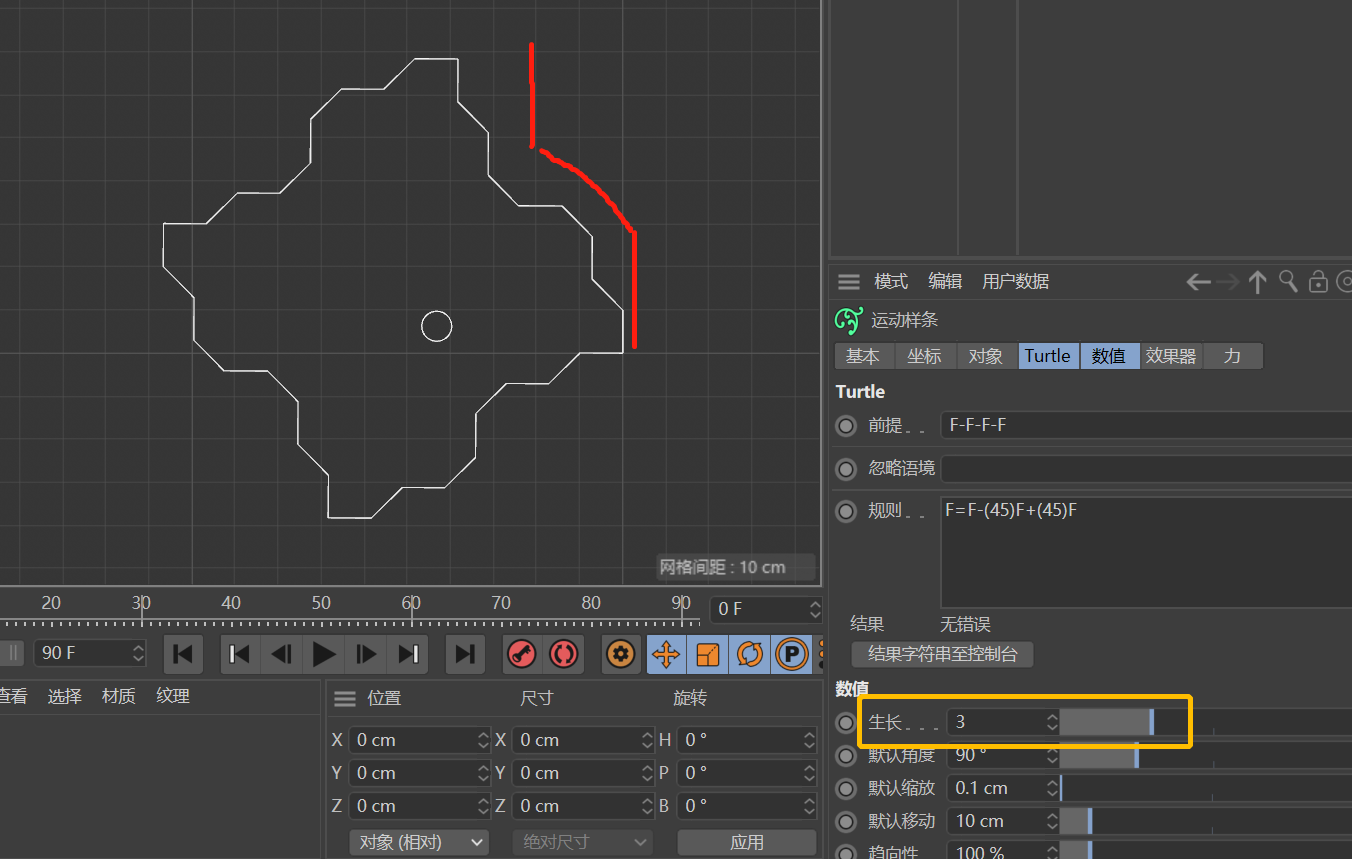
这不就是分形迭代吗！「生长」数值就是迭代次数（n）。

再举个例子，「前提」为F--F--F，「默认角度」改为60°，得到的是一个正三角形。

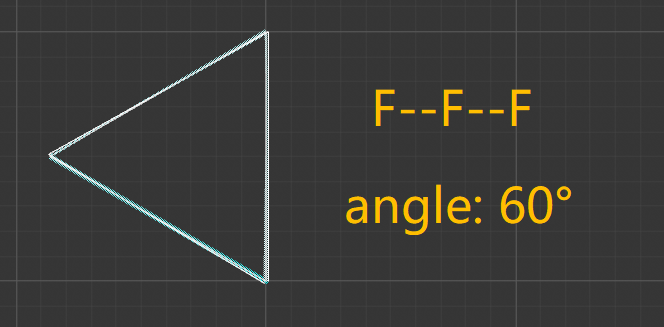
然后将「规则」设为F=F+F--F+F，「生长」值（即迭代次数）为2时得到的是一个六角星形。

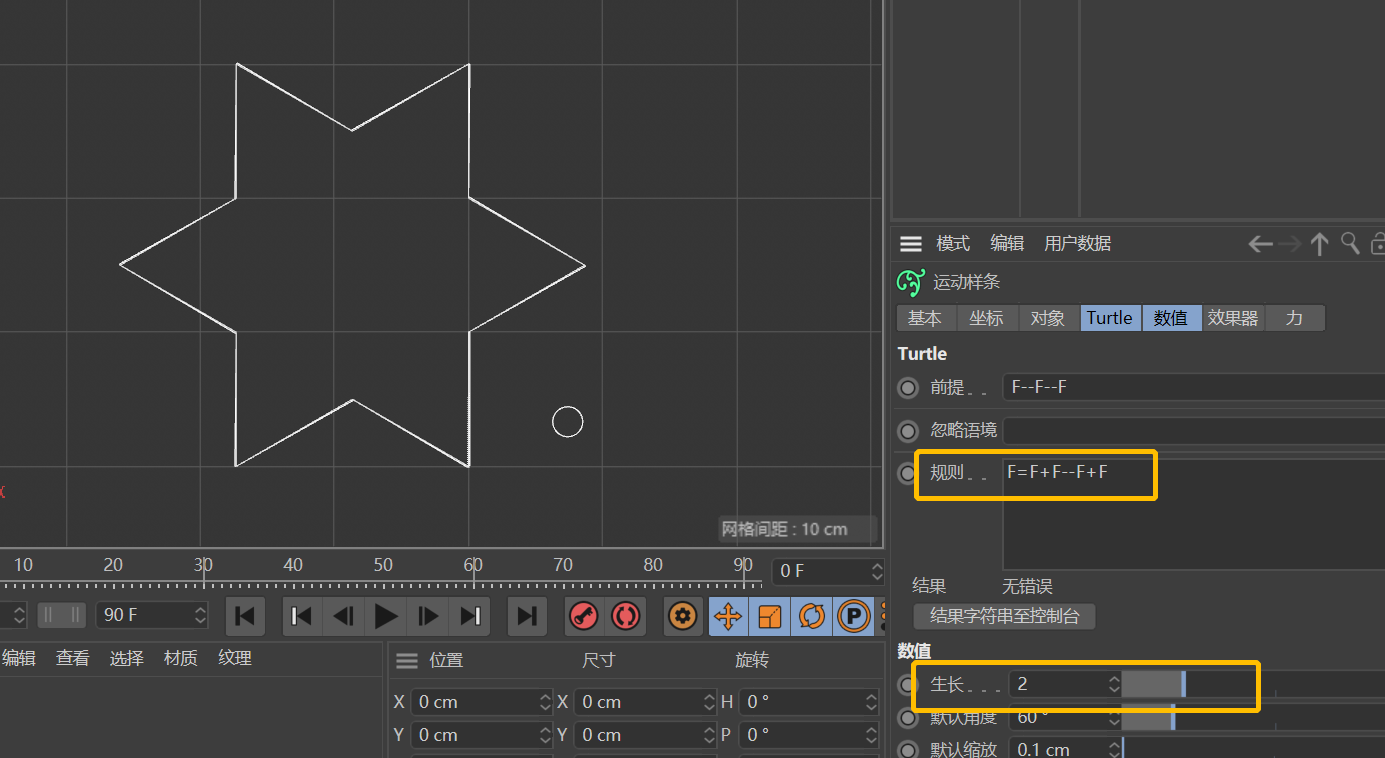
继续增加「生长」值，得到的曲线形状如下。如果你对分形略有了解，应该可以看出这就是科赫曲线，也叫科赫雪花。

类似的我们可以画出各种分形曲线，仅以「前提」F-F-F-F为例，在不同的「规则」下，可以得到以下形状（「默认角度」均为90°）：

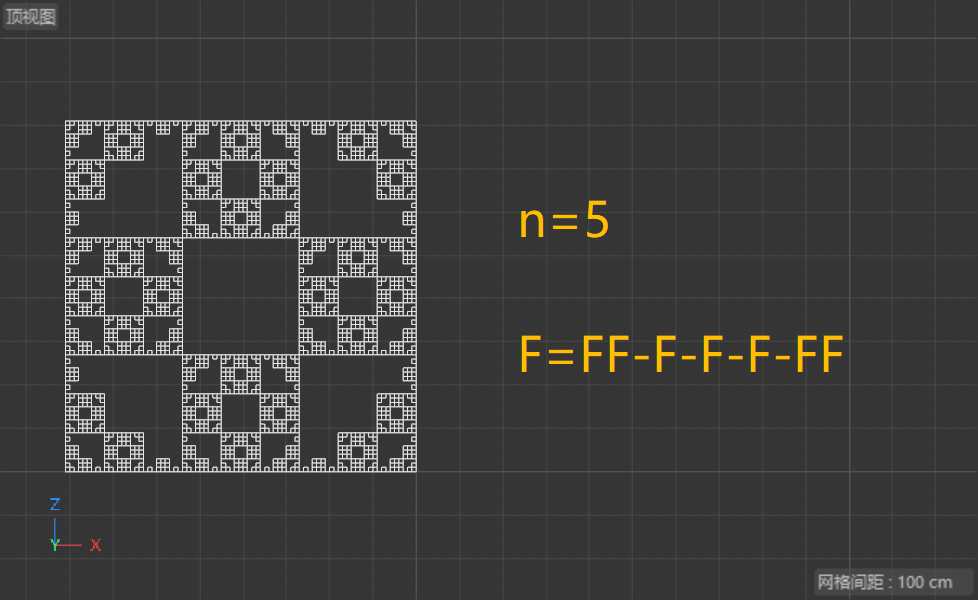
在有些情况下，规则可能不止一条，如：

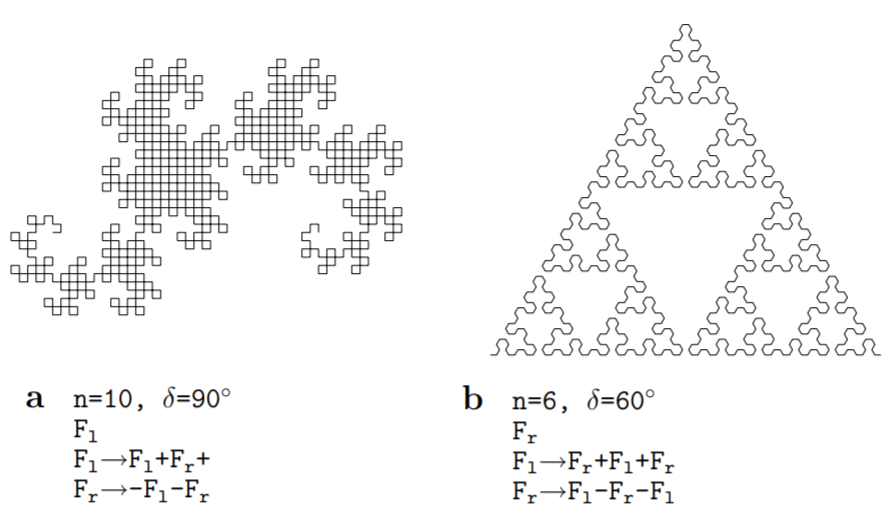
图片源自The Algorithmic Beauty of Plants, pp 11.

这里的Fl和Fr其实就是F的意思，只不过为了区分，分别用l和r进行标记。比如上面的a图中，「前提」就是F，「规则」有两条，分别为：

Fl=Fl+Fr+

Fr=-Fl-Fr

每次迭代只需将Fl和Fr按照上述规则进行替换即可。

迭代次数为0时，图形为Fl，即F；

迭代次数为1时，图形为Fl+Fr+，即F+F+；

迭代次数为2时，图形为Fl+Fr++-Fl-Fr+，即F+F+F-F+；

……

在C4D中，这里的写法稍微要注意一下。「前提」可写为FA，「规则」分别为A=A+BF+和B=-FA-B（Lindenmayer在他的书中有推导，感兴趣的同学可以自行查看，书名见上图底部标注）。这里的A和B没有具体含义，只作为替换变量使用。

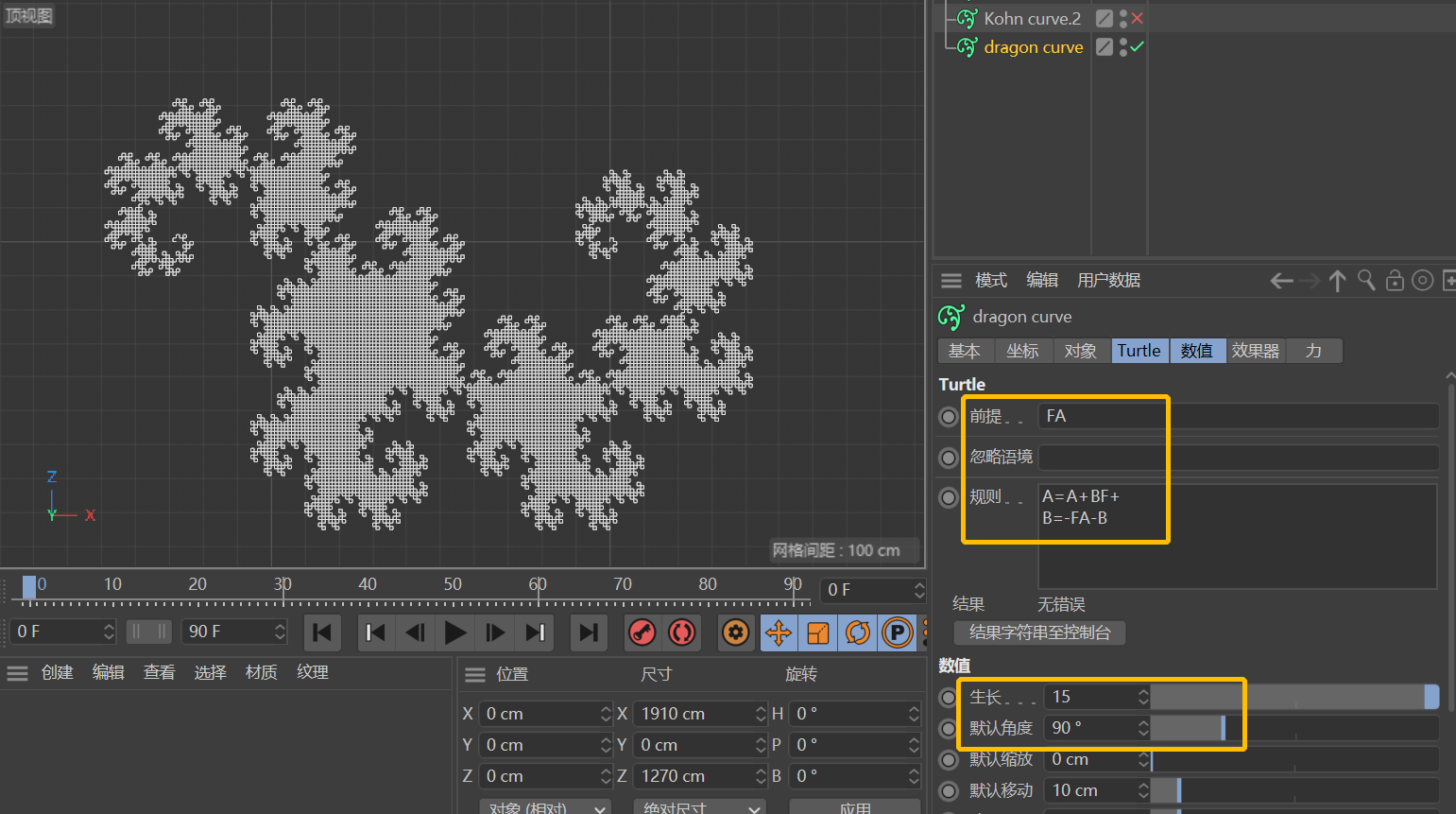
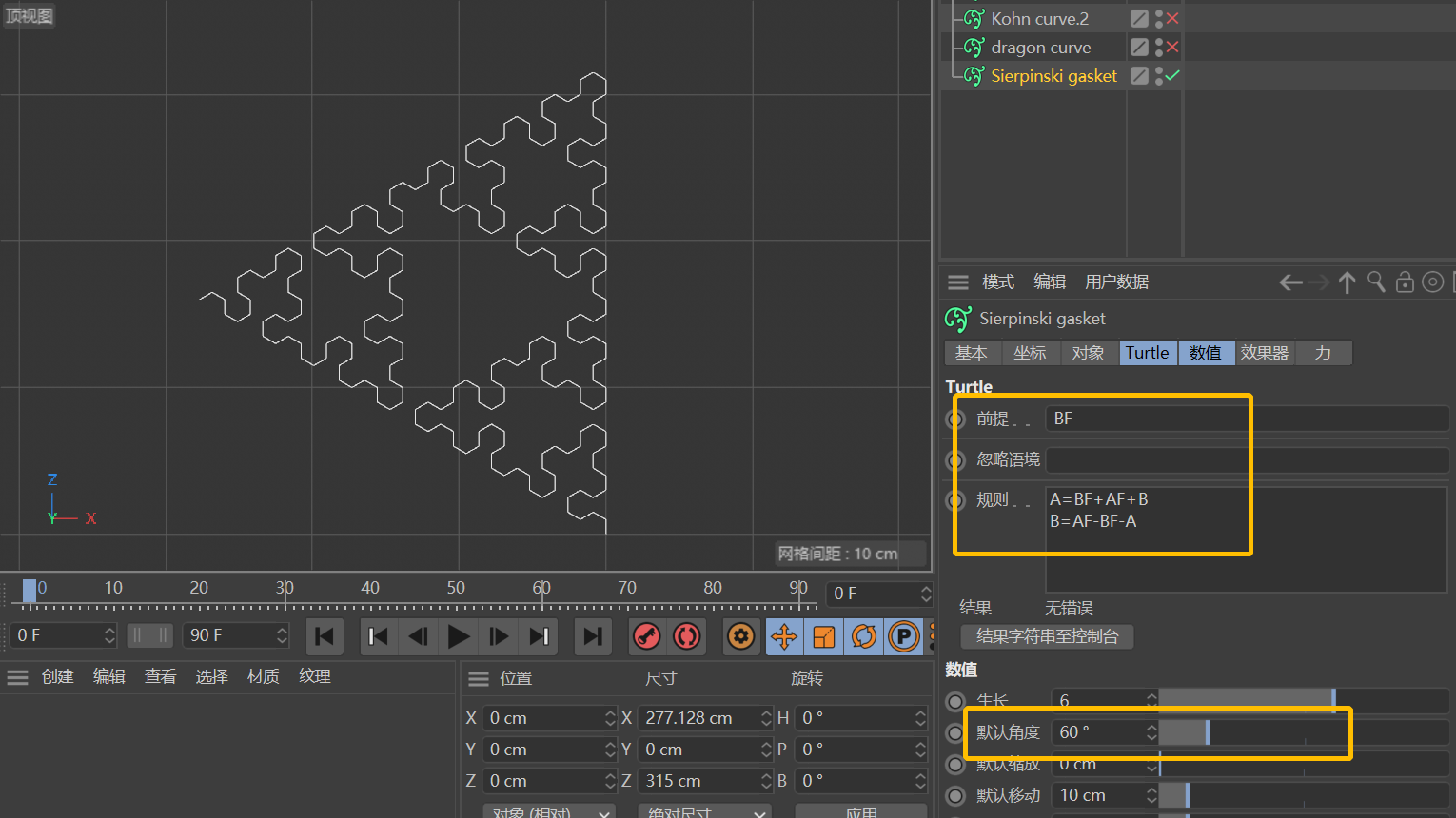
类似地，上面b图中的Sierpinski gasket可以表述为「前提」：BF，「规则」：A=BF+AF+B和B=AF-BF-A。（「默认角度」为60°）

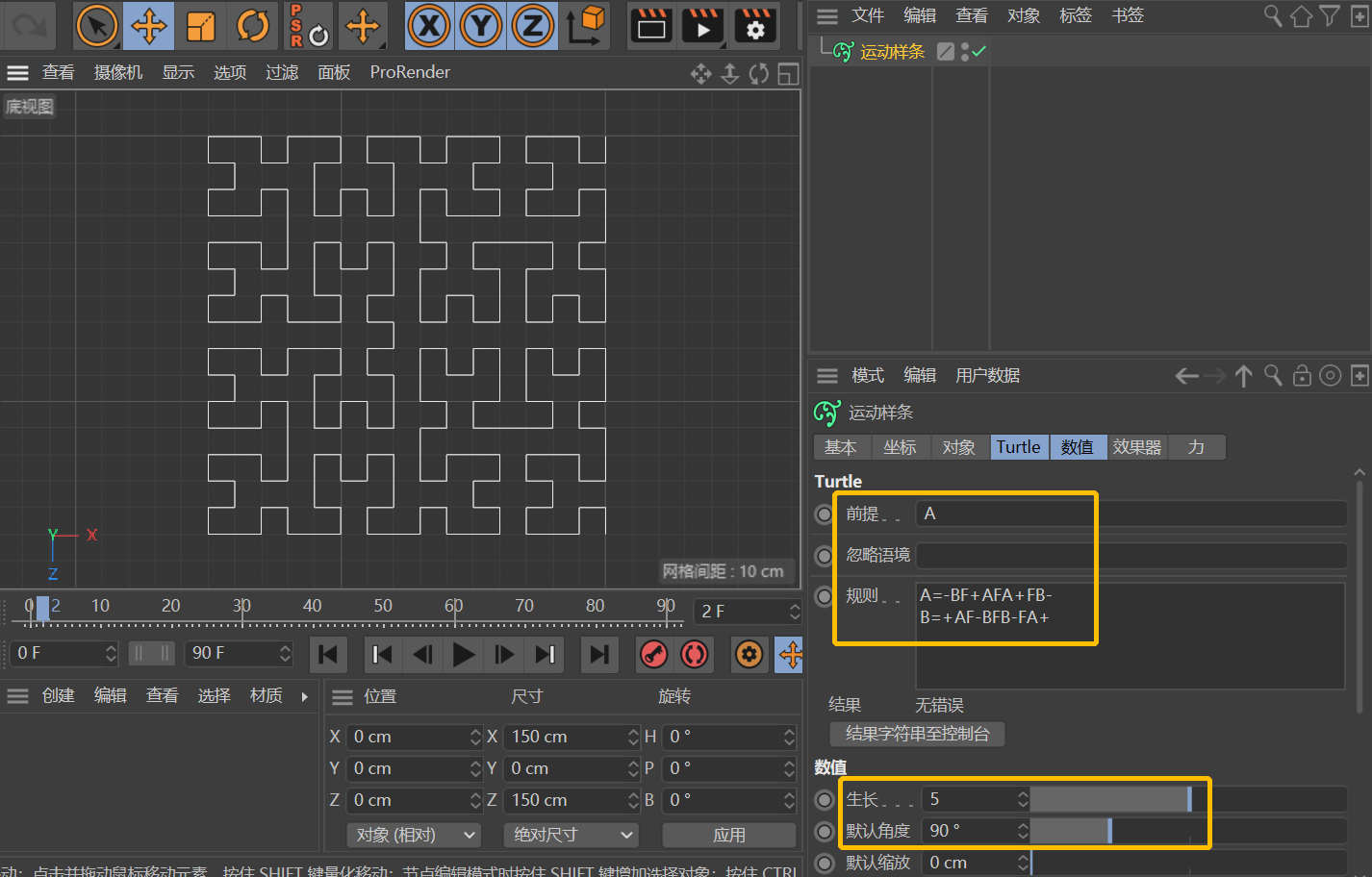
再比如，「前提」为A，「规则」为A=-BF+AFA+FB-和B=+AF-BFB-FA+，迭代后就可以得到Hilbert曲线。（「默认角度」为90°）

为了留时间给你们消化，本期教程就讲到这里。相信大家对L-systems已经有了初步的了解，如果有兴趣的话后面我还会介绍怎么用运动样条做各种分叉效果，来模拟不同的植物。

BIM技术是未来的趋势，学习、了解掌握更多BIM前言技术是大势所趋，欢迎更多BIMer加入BIM中文网大家庭（http://www.wanbim.com），一起共同探讨学习BIM技术，了解BIM应用！