本文概述:CAD弧长计算是计算机辅助设计中的重要一环,其准确性和效率直接影响到设计产品的质量和生产成本。传统的CAD弧长计算方法具有一定的局限性,因此需要进行优化以提高精度和速度。
在现代
(CAD)系统中,弧长计算是许多功能模块的基础工作之一。设计者在创建复杂曲线时,需要知道曲线的长度以便于后续加工过程中的材料估算、路径规划等。然而,传统的弧长计算方法通常依赖于数值积分或者简单的几何解析方法,这些方法可能会在精度上存在欠缺,尤其是对于高度复杂的曲线。首先,我们来看一下弧长计算的基本原理。对于一个给定的曲线,可以通过积分的方式来计算它的弧长。如果我们把曲线参数化为r(t),那么弧长L可以表示为: \[L = \int_{a}^{b} \| r'(t) \| dt\]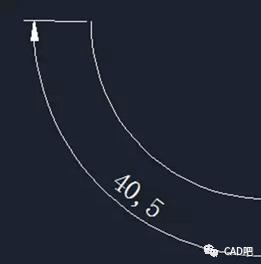
参数化
曲线本身可能非常复杂,所以这个积分表达式通常不能用简单的解析公式来解决。这就引出了一个常见的数值解法——。数值积分有很多算法,诸如梯形规则、辛普森规则以及高阶的Gauss-Kronrod规则等。每种方法都有其最佳应用场景,但它们共同的特点是:随着分段细化,它们的精度会相应提高,同时计算量也增加。
优化方法
之一是采用自适应积分。自适应积分根据函数的变化自动调整分段的数量,使得在变化较大的区间使用更多的分段,而在变化较小的区间使用较少的分段。这种方法能够有效地平衡计算精度和运算速度。但这种方法最大的挑战在于合理的误差控制机制,即如何在计算过程中动态调整分段以保持精度。另一个值得关注的优化策略是基于的弧长计算。这包括选取适当的样条函数进行曲线拟合,通过这些拟合函数来简化弧长计算。常见的方法例如B样条拟合和NURBS(非均匀有理B样条),这些技术允许对不规则曲线进行良好的逼近,而且能够快速计算弧长。此外,CAD系统还可以利用和GPU加速来提升弧长计算的速度。通过并行计算,将大数据量的处理分散到多个计算单元上进行协同处理,大大减少了计算时间。同时,使用GPU进行图形运算,可以进一步提高速度,因为GPU的架构特别适合处理大量相同类型的计算任务。在工业实践中,选择合适的优化方法需要考虑具体的应用场景和约束条件。例如,对于实时要求很高的环境,如航空制造和汽车设计,可能需要更倾向于快速响应的优化方法。而在需要极高精度的场合,例如微电子设计,可能需要优先考虑那些能够提供更高精度的算法。综上所述,CAD弧长计算的优化不仅仅局限于算法本身,还涉及到整个系统的改良,包括数值方法的选择、硬件加速的利用以及针对特定应用的特殊处理等等。随着现代技术的发展,这些优化方法正变得越来越重要,并且将在未来继续发挥关键作用。希望通过此说明能够帮助读者理解CAD弧长计算优化的复杂性以及如何在实际操作中应用这些技术。
BIM技术是未来的趋势,学习、了解掌握更多BIM前言技术是大势所趋,欢迎更多BIMer加入BIM中文网大家庭(http://www.wanbim.com),一起共同探讨学习BIM技术,了解BIM应用!

