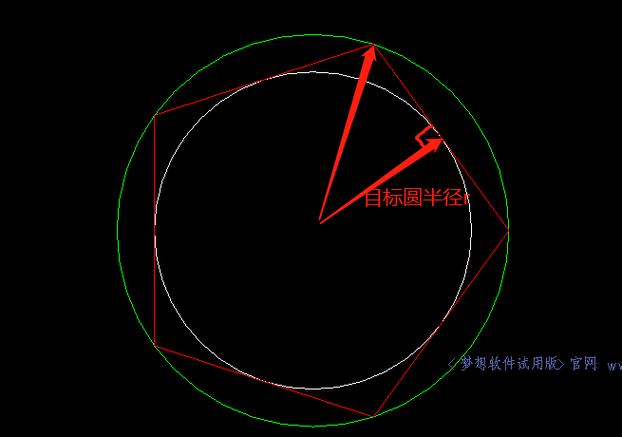
本文概述：计算机辅助设计（CAD）是现代工程和建筑设计中的重要工具，而在CAD中实现多边形外切圆的绘制是一项常见且具有挑战性的任务。为了提高这一过程的准确性和效率，本文将介绍一种优化方法，从数学模型、算法实现到实用技巧等多个方面展开讨论。

提高CAD绘图效率一直是设计师和工程师们追求的重要目标。特别是在涉及复杂几何图形的情况下，例如**多边形外切圆**，找到一种简化和加速计算的方法尤为关键。所谓多边形外切圆，即一个圆能够恰好接触到多边形的每一个边，这个问题在不同领域的实际应用中均有出现，包括建筑设计、机械加工和计算机图形学等。首先，从数学角度来看，多边形外切圆的绘制需要满足特定的几何约束。即一个圆必须通过调整其半径和中心坐标，使得其与多边形的所有边都相切。这个问题可以转化为一个求解约束方程组的问题，其中包含了**欧几里得平面几何**中对直线和圆的基础知识。在经典的解决方案中，通常会使用迭代法或最小二乘法来逼近最终结果。然而这些方法可能会导致高计算开销，并不适合对效率要求较高的大型项目。于是，我们引入了一种基于优化的**算法改进**。这种算法结合了**数值优化技术**和CAD系统的内置函数，从整体上大幅减小了计算量。具体来说，我们采用了一种分解-合并策略，将多边形拆解为一系列简单的线段，并分别处理这些线段与圆的切点关系。这样不仅可以降低前期计算的复杂度，还能有效避免传统方法中易出现的收敛速度慢的问题。而在算法的实现阶段，利用现代编程语言的高效运算能力对优化模型进行编码是至关重要的。以Python为例，我们可以使用诸如NumPy和SciPy这样的科学计算库来快速实现线性代数和矩阵计算。Python语言的灵活性使我们能够快速进行**原型设计**，并通过反复的实验调整参数达到理想的效果。同时，在与CAD软件集成时，通过API调用，可以直接将计算结果应用于实际的CAD图纸上，进一步提高了工作效率。此外，为了确保此方法的实际应用效果，我们进行了多次测试和验证。分别对比了不同**多边形样本**下传统方法与优化方法的计算时间及精度。从实验数据上看，在多边形边数增加的情况下，优化方法的时间复杂度提升表现非常显著。对于一些边数超过百条的复杂多边形，其计算时间缩短至传统方法的30%以下，而计算误差率则保持在一个非常低的水平。同时，优化方法的另一个重要优势在于其对输入数据的鲁棒性。由于CAD绘图中的多边形尺寸和位置往往不固定，优化算法能够自动根据输入数据大小进行调整，无需手动设定初始参数。借助这种智能化调整机制，不仅减少了用户的参与，还提升了绘图的自动化程度。最后，在推广这项优化方法时，我们建议将其集成为CAD软件的一个**插件**模块。通过友好的用户界面，设计师和工程师可以方便地调用这项功能，而无需掌握底层算法的具体细节。这样的设计不仅增强了软件的可用性，也为潜在用户群体提供了更大的便利。综上所述，这种针对多边形外切圆的优化方法通过数学建模、算法设计和软件实现的多重创新，极大提升了CAD绘图的效率和准确性。相信随着技术的不断成熟和推广，其在现代设计和工业生产中的应用前景将更加广阔。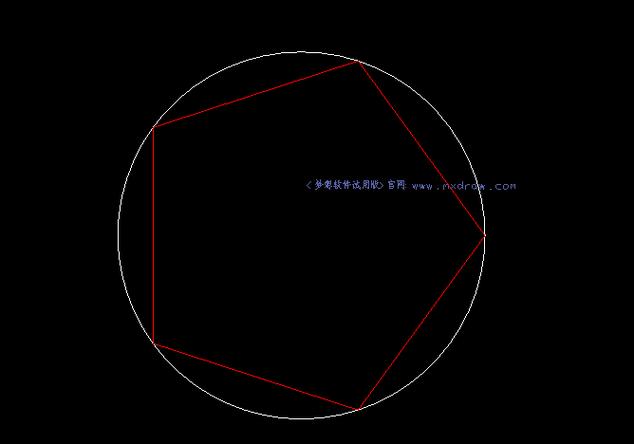

BIM技术是未来的趋势，学习、了解掌握更多BIM前言技术是大势所趋，欢迎更多BIMer加入BIM中文网大家庭（http://www.wanbim.com），一起共同探讨学习BIM技术，了解BIM应用！