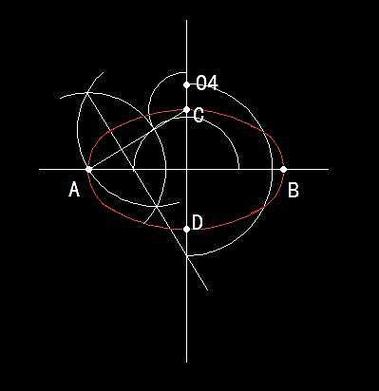
本文概述：椭圆是几何中的重要图形之一，其绘制方法在数学和工程领域都有广泛应用。利用“四个中心点”来绘制椭圆是一种有效且精确的方法，它能够帮助我们理解椭圆的结构，并通过简单步骤实现椭圆的描绘。

在绘制椭圆时，我们经常需要一些技巧来确保图形的准确性和美观。“四个中心点法”就是这样一种用于绘制椭圆的实用方法。这种方法主要基于椭圆的数学特性，由其长轴、短轴以及它们的焦点位置决定了椭圆的基本结构。首先，我们需要理解椭圆的**基本性质**。椭圆是平面上到两个焦点距离之和为定值的点构成的轨迹。通常，椭圆的长轴是经过两个焦点的一条线段，而短轴垂直于长轴并穿过椭圆的中心。这样的定义使得椭圆在坐标系中具有明确的位置和方向。使用“四个中心点法”绘制椭圆的过程可以分为几个步骤。首先，我们确定椭圆的中心及其长轴和短轴的长度。在实际操作中，我们可以先设定一个坐标系，并确保椭圆的中心位于某个特定点，这样便于后续计算和调整。接下来，我们需要找出椭圆的四个关键点。首先是**顶点**，即长轴两端的两个点，这些点表示椭圆最宽的部分。然后是次顶点，即短轴两端的两个点，这些点表示椭圆最高的部分。通过这四个点，我们可以初步形成椭圆的大致框架。利用这些中心点，我们可以开始绘制椭圆的曲线轮廓。通常情况下，我们会使用专业的绘图工具或软件，通过逐渐连接这些中心点的方式形成一个闭合的曲线。这时候，在图形软件中应用适当的曲线调整功能，可以确保椭圆的光滑性以及曲线的自然过渡。在更详细的计算中，椭圆的方程也可以帮助我们进一步确认椭圆的正确性。应用标准的椭圆公式，我们可以验证所绘椭圆是否符合其参数设定。这一方程通常以中心点协调表示为(h, k)，而长轴长度为a，短轴长度为b。其标准公式为((x-h)^2)/a^2 + ((y-k)^2)/b^2 = 1，这一表达形式允许我们检查绘制椭圆的每一点是否符合预期的数学关系。运用椭圆方程在实际测量中也十分有用。对于那些从事结构设计或建筑工作的人而言，利用这种方法不仅能够精确地复刻复杂图形，还能确保按照设计计划进行校验和调整。此外，为了提高椭圆绘制的效率和精度，很多软件提供了自动化工具和插件供用户选择。这些工具通常可以根据输入的中心点和轴数值，自动生成一个完美的椭圆，这些**优化工具**让绘制过程变得更加简单和高效。总之，“四个中心点法”是一种直观且方便的椭圆绘制技巧，通过结合数学理论和实践操作，使得这一方法在不论是教育还是工业应用中，都能发挥显著作用。通过掌握这种方法，我们可以充分认识椭圆这一几何图形的内在规律，同时提高我们的绘图技能。无论是在手动绘制还是数字化设计中，这种方法都能提供有效的指导。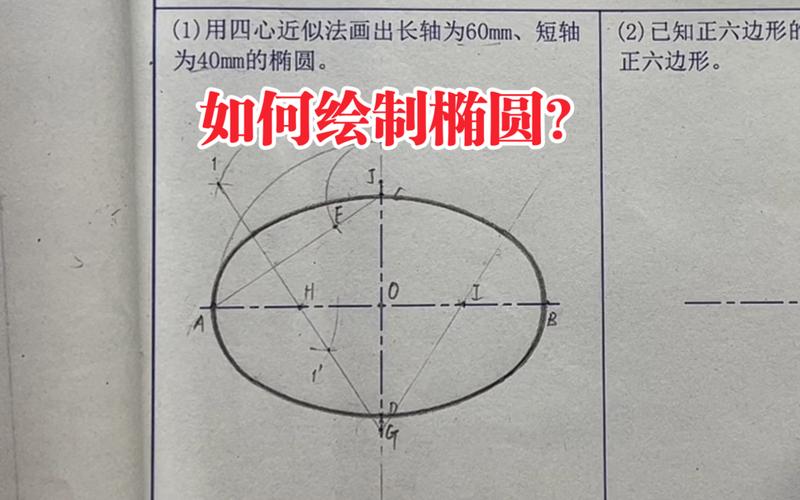

BIM技术是未来的趋势，学习、了解掌握更多BIM前言技术是大势所趋，欢迎更多BIMer加入BIM中文网大家庭（http://www.wanbim.com），一起共同探讨学习BIM技术，了解BIM应用！